Reflections
Learning Outcomes
- Graph functions using reflections about the [latex]x[/latex] -axis and the [latex]y[/latex] -axis.
- Determine whether a function is even, odd, or neither from its graph.
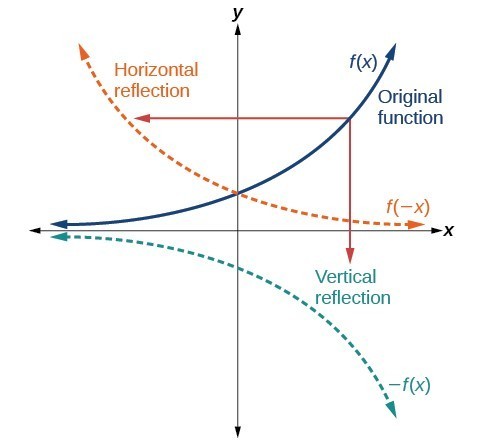 Vertical and horizontal reflections of a function.
Vertical and horizontal reflections of a function.A General Note: Reflections
Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=-f\left(x\right)[/latex] is a vertical reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about (or over, or through) the [latex]x[/latex]-axis. Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(-x\right)[/latex] is a horizontal reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about the [latex]y[/latex]-axis.How To: Given a function, reflect the graph both vertically and horizontally.
- Multiply all outputs by –1 for a vertical reflection. The new graph is a reflection of the original graph about the [latex]x[/latex]-axis.
- Multiply all inputs by –1 for a horizontal reflection. The new graph is a reflection of the original graph about the [latex]y[/latex]-axis.
Example: Reflecting a Graph Horizontally and Vertically
Reflect the graph of [latex]s\left(t\right)=\sqrt{t}[/latex] (a) vertically and (b) horizontally.Answer: a. Reflecting the graph vertically means that each output value will be reflected over the horizontal [latex]t[/latex]-axis as shown below.
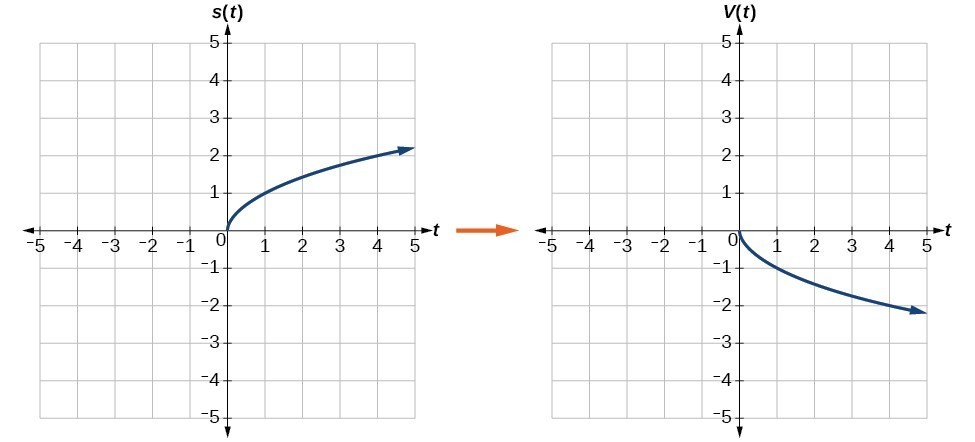 Vertical reflection of the square root function
Vertical reflection of the square root function[latex]V\left(t\right)=-s\left(t\right)\text{ or }V\left(t\right)=-\sqrt{t}[/latex]
Notice that this is an outside change, or vertical shift, that affects the output [latex]s\left(t\right)[/latex] values, so the negative sign belongs outside of the function. b. Reflecting horizontally means that each input value will be reflected over the vertical axis as shown below.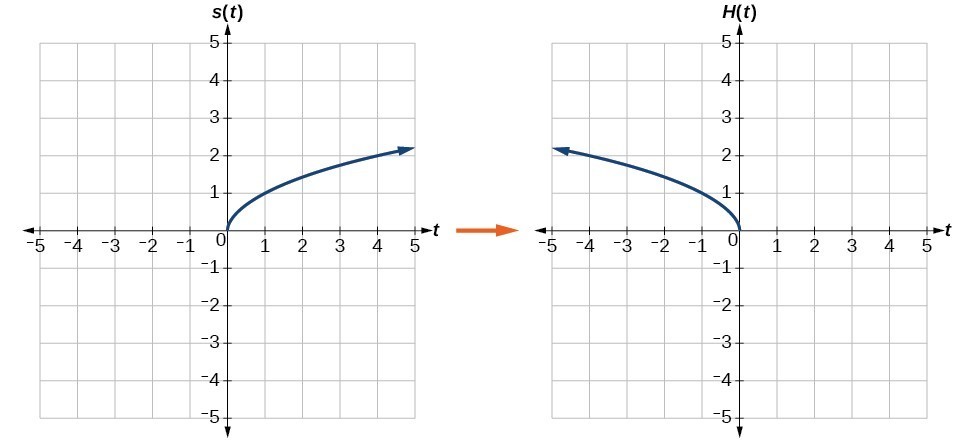 Horizontal reflection of the square root function
Horizontal reflection of the square root function[latex]H\left(t\right)=s\left(-t\right)\text{ or }H\left(t\right)=\sqrt{-t}[/latex]
Notice that this is an inside change or horizontal change that affects the input values, so the negative sign is on the inside of the function. Note that these transformations can affect the domain and range of the functions. While the original square root function has domain [latex]\left[0,\infty \right)[/latex] and range [latex]\left[0,\infty \right)[/latex], the vertical reflection gives the [latex]V\left(t\right)[/latex] function the range [latex]\left(-\infty ,0\right][/latex] and the horizontal reflection gives the [latex]H\left(t\right)[/latex] function the domain [latex]\left(-\infty ,0\right][/latex].Try It
Use an online graphing calculator to reflect the graph of [latex]f\left(x\right)=|x - 1|[/latex] (a) vertically and (b) horizontally.Answer:
a)
 b)
b)

Example: Reflecting a Tabular Function Horizontally and Vertically
A function [latex]f\left(x\right)[/latex] is given. Create a table for the functions below.- [latex]g\left(x\right)=-f\left(x\right)[/latex]
- [latex]h\left(x\right)=f\left(-x\right)[/latex]
| [latex]x[/latex] | 2 | 4 | 6 | 8 |
| [latex]f\left(x\right)[/latex] | 1 | 3 | 7 | 11 |
Answer:
- For [latex]g\left(x\right)[/latex], the negative sign outside the function indicates a vertical reflection, so the [latex]x[/latex]-values stay the same and each output value will be the opposite of the original output value.
[latex]x[/latex] 2 4 6 8 [latex]g\left(x\right)[/latex] –1 –3 –7 –11 - For [latex]h\left(x\right)[/latex], the negative sign inside the function indicates a horizontal reflection, so each input value will be the opposite of the original input value and the [latex]h\left(x\right)[/latex] values stay the same as the [latex]f\left(x\right)[/latex] values.
[latex]x[/latex] −2 −4 −6 −8 [latex]h\left(x\right)[/latex] 1 3 7 11
Try It
| [latex]x[/latex] | −2 | 0 | 2 | 4 |
| [latex]f\left(x\right)[/latex] | 5 | 10 | 15 | 20 |
Answer:
- [latex]g\left(x\right)=-f\left(x\right)[/latex]
[latex]x[/latex] -2 0 2 4 [latex]g\left(x\right)[/latex] [latex]-5[/latex] [latex]-10[/latex] [latex]-15[/latex] [latex]-20[/latex] - [latex]h\left(x\right)=f\left(-x\right)[/latex]
[latex]x[/latex] -2 0 2 4 [latex]h\left(x\right)[/latex] 15 10 5 unknown
Determine Whether a Functions is Even, Odd, or Neither
Some functions exhibit symmetry so that reflections result in the original graph. For example, horizontally reflecting the toolkit functions [latex]f\left(x\right)={x}^{2}[/latex] or [latex]f\left(x\right)=|x|[/latex] will result in the original graph. We say that these types of graphs are symmetric about the [latex]y[/latex]-axis. Functions whose graphs are symmetric about the y-axis are called even functions. If the graphs of [latex]f\left(x\right)={x}^{3}[/latex] or [latex]f\left(x\right)=\dfrac{1}{x}[/latex] were reflected over both axes, the result would be the original graph.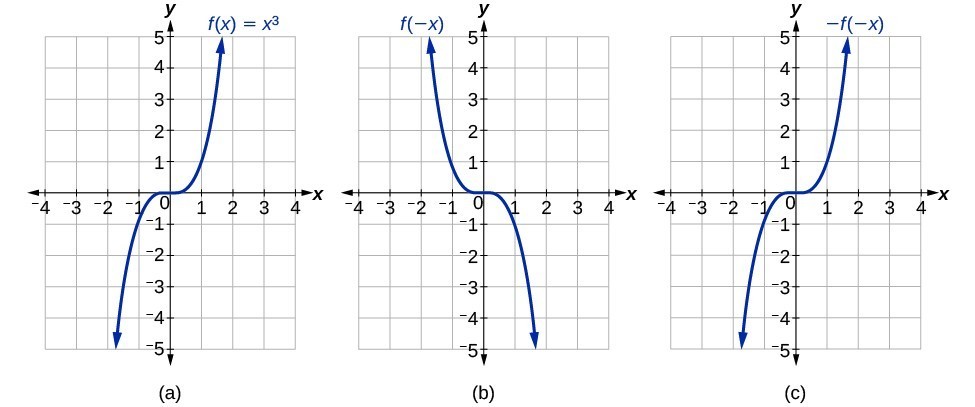 (a) The cubic toolkit function (b) Horizontal reflection of the cubic toolkit function (c) Horizontal and vertical reflections reproduce the original cubic function.
(a) The cubic toolkit function (b) Horizontal reflection of the cubic toolkit function (c) Horizontal and vertical reflections reproduce the original cubic function.A General Note: Even and Odd Functions
A function is called an even function if for every input [latex]x[/latex] [latex-display]f\left(x\right)=f\left(-x\right)[/latex-display] The graph of an even function is symmetric about the [latex]y\text{-}[/latex] axis. A function is called an odd function if for every input [latex]x[/latex] [latex-display]f\left(x\right)=-f\left(-x\right)[/latex-display] The graph of an odd function is symmetric about the origin.How To: Given the formula for a function, determine if the function is even, odd, or neither.
- Determine whether the function satisfies [latex]f\left(x\right)=f\left(-x\right)[/latex]. If it does, it is even.
- Determine whether the function satisfies [latex]f\left(x\right)=-f\left(-x\right)[/latex]. If it does, it is odd.
- If the function does not satisfy either rule, it is neither even nor odd.
recall evaluating functions
When evaluating functions for specific input, we can wrap the variable in parentheses first, then drop in the value we want to use to evaluate it. This works whether the value is a constant or a variable. Be extra careful when evaluating a function for a negative input. The negative sign goes in the parentheses. Ex. Evaluate [latex]f(x) = x^2 \ \text{ for} -1[/latex] [latex-display]\begin{align} f(-1) &= (-1)^2 \\ &= 1 \end{align}[/latex-display]Example: Determining whether a Function Is Even, Odd, or Neither
Is the function [latex]f\left(x\right)={x}^{3}+2x[/latex] even, odd, or neither?Answer: Without looking at a graph, we can determine whether the function is even or odd by finding formulas for the reflections and determining if they return us to the original function. Let’s begin with the rule for even functions.
[latex]f\left(-x\right)={\left(-x\right)}^{3}+2\left(-x\right)=-{x}^{3}-2x[/latex]
This does not return us to the original function, so this function is not even. We can now test the rule for odd functions.[latex]-f\left(-x\right)=-\left(-{x}^{3}-2x\right)={x}^{3}+2x[/latex]
Because [latex]-f\left(-x\right)=f\left(x\right)[/latex], this is an odd function.Analysis of the Solution
Consider the graph of [latex]f[/latex]. Notice that the graph is symmetric about the origin. For every point [latex]\left(x,y\right)[/latex] on the graph, the corresponding point [latex]\left(-x,-y\right)[/latex] is also on the graph. For example, (1, 3) is on the graph of [latex]f[/latex], and the corresponding point [latex]\left(-1,-3\right)[/latex] is also on the graph.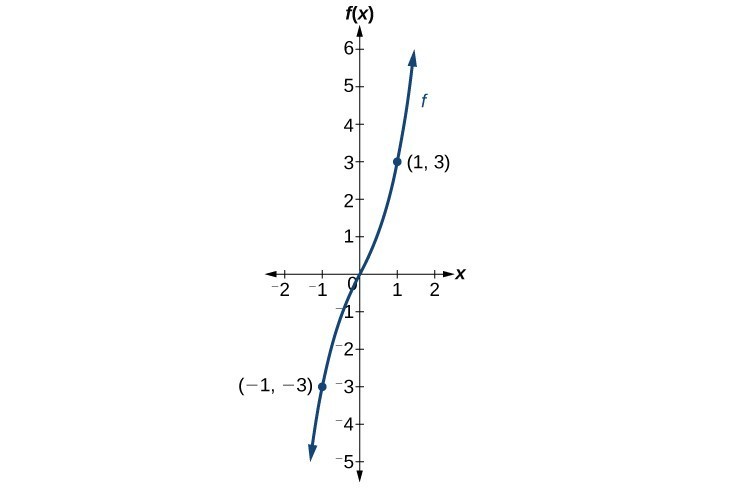
Try It
Is the function [latex]f\left(s\right)={s}^{4}+3{s}^{2}+7[/latex] even, odd, or neither?Answer: Even
[ohm_question]112703[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Question ID 112701, 60650, 113454,112703. Authored by: Lumen Learning. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].

