Terms of an Arithmetic Sequence
Learning Objectives
- Find the common difference for an arithmetic sequence
- Find terms of an arithmetic sequence
The values of the truck in the example are said to form an arithmetic sequence because they change by a constant amount each year. Each term increases or decreases by the same constant value called the common difference of the sequence. For this sequence, the common difference is –3,400.
The sequence below is another example of an arithmetic sequence. In this case, the constant difference is 3. You can choose any term of the sequence, and add 3 to find the subsequent term.
A General Note: Arithmetic Sequence
An arithmetic sequence is a sequence that has the property that the difference between any two consecutive terms is a constant. This constant is called the common difference. If [latex]{a}_{1}[/latex] is the first term of an arithmetic sequence and [latex]d[/latex] is the common difference, the sequence will be: [latex-display]\left\{{a}_{n}\right\}=\left\{{a}_{1},{a}_{1}+d,{a}_{1}+2d,{a}_{1}+3d,...\right\}[/latex-display]Example: Finding Common Differences
Is each sequence arithmetic? If so, find the common difference.- [latex]\left\{1,2,4,8,16,...\right\}[/latex]
- [latex]\left\{-3,1,5,9,13,...\right\}[/latex]
Answer: Subtract each term from the subsequent term to determine whether a common difference exists.
- The sequence is not arithmetic because there is no common difference.
- The sequence is arithmetic because there is a common difference. The common difference is 4.
Analysis of the Solution
The graph of each of these sequences is shown in Figure 1. We can see from the graphs that, although both sequences show growth, [latex]a[/latex] is not linear whereas [latex]b[/latex] is linear. Arithmetic sequences have a constant rate of change so their graphs will always be points on a line.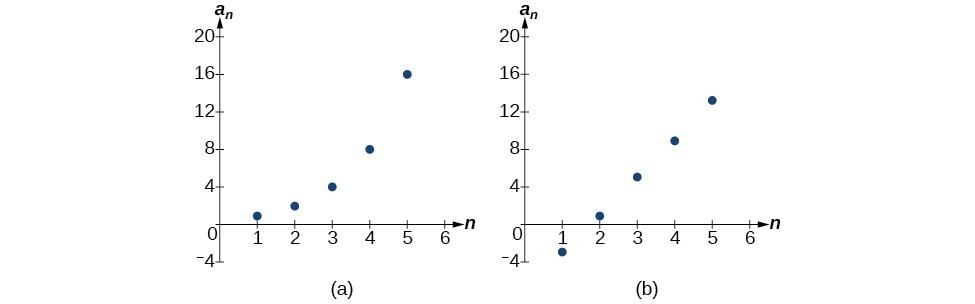
Q & A
If we are told that a sequence is arithmetic, do we have to subtract every term from the following term to find the common difference?
No. If we know that the sequence is arithmetic, we can choose any one term in the sequence, and subtract it from the subsequent term to find the common difference.Try It
Is the given sequence arithmetic? If so, find the common difference.[latex]\left\{18,\text{ }16,\text{ }14,\text{ }12,\text{ }10,\dots \right\}[/latex]
Answer: The sequence is arithmetic. The common difference is [latex]-2[/latex].
How To: Given any the first term and any other term in an arithmetic sequence, find a given term.
- Substitute the values given for [latex]{a}_{1},{a}_{n},n[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex] to solve for [latex]d[/latex].
- Find a given term by substituting the appropriate values for [latex]{a}_{1},n[/latex], and [latex]d[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex].
Example: Writing Terms of Arithmetic Sequences
Given [latex]{a}_{1}=8[/latex] and [latex]{a}_{4}=14[/latex] , find [latex]{a}_{5}[/latex] .Answer: The sequence can be written in terms of the initial term 8 and the common difference [latex]d[/latex] .
[latex]\left\{8,8+d,8+2d,8+3d\right\}[/latex]
We know the fourth term equals 14; we know the fourth term has the form [latex]{a}_{1}+3d=8+3d[/latex] . We can find the common difference [latex]d[/latex] .[latex]\begin{array}{ll}{a}_{n}={a}_{1}+\left(n - 1\right)d\hfill & \hfill \\ {a}_{4}={a}_{1}+3d\hfill & \hfill \\ {a}_{4}=8+3d\hfill & \text{Write the fourth term of the sequence in terms of } {a}_{1} \text{ and } d.\hfill \\ 14=8+3d\hfill & \text{Substitute } 14 \text{ for } {a}_{4}.\hfill \\ d=2\hfill & \text{Solve for the common difference}.\hfill \end{array}[/latex]
Find the fifth term by adding the common difference to the fourth term.[latex]{a}_{5}={a}_{4}+2=16[/latex]
Analysis of the Solution
Notice that the common difference is added to the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by adding the common difference to the first term nine times or by using the equation [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex].Try It
Given [latex]{a}_{3}=7[/latex] and [latex]{a}_{5}=17[/latex] , find [latex]{a}_{2}[/latex] .Answer: [latex]{a}_{2}=2[/latex]
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Question ID 5847, 5832. Authored by: Web-Work Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 23735. Authored by: Roy Shahbazian. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
