Circles
Recall from Geometry that a circle can be determined by fixing a point (called the center) and a positive number (called the radius) as follows.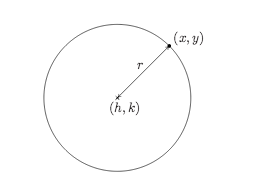 From the picture, we see that a point (x,y) is on the circle if and only if its distance to (h,k) is r.
From the picture, we see that a point (x,y) is on the circle if and only if its distance to (h,k) is r.[latex]{ r }=\sqrt{{\left(x - h\right)}^{2}+{\left(y - k\right)}^{2}}\\[/latex]
By squaring both sides of this equation we get an equivalent equation (since r > 0) which gives us the standard equation of a circle.The Standard Equation of a Circle
The equation of a circle with center (h,k) and raduis r > 0 is
[latex]{\left(x - h\right)}^{2}+{\left(y - k\right)}^{2}={r}^{2}\\[/latex]
Example 1: Write the Standard Equation of a Circle given the center and a radius.
Write the standard equation of the circle whose center is ( -2,3) and whose radius is 5.Solution
Here, (h,k) = (-2, 3) and r = 5, so we get:
[latex-display]\begin{array}{rrr}{\left(x-\left(-2\right)\right)}^{2}+{\left(y-3\right)}^{2}& \hfill = &\hfill{\left(5\right)}^{2}\\{\left(x+2\right)}^{2}+{\left(y-3\right)}^{2}& \hfill = &\hfill{25}\end{array}\\[/latex-display]Example 2: Graph a circle given an equation in standard form.
Graph [latex]{\left(x+2\right)}^{2}+{\left(y-1\right)}^{2}={ 4 }\\[/latex]. Find the center and radius.Solution
From the standard equation of a circle, we have that [latex]{\left(x+2\right)}\\[/latex] is [latex]{\left(x-h\right)}\\[/latex], so h = -2 and [latex]{\left(y-1\right)}\\[/latex] is [latex]{\left(y-k\right)}\\[/latex] so k = 1. This tells us that our center is (-2, 1). Furthermore, [latex]{r}^{2} = {4}\\[/latex], so r = 2. Graphing gives us- Group the same variables together on one side of the equation and position the constant on the other side.
- Complete the square on both variables as needed.
- Divide both sides by the coefficient of the squares. (For circles, they will be the same).
Example 3: Complete the square to find the center and radius of a circle whose equation is not in standard form.
Find the center and radius of the circle whose equation is [latex]3{x}^{2}-6x+3{y}^{2} +4y-4=0\\[/latex]Solution
[latex-display]\begin{array}{cccc}3{x}^{2}-6x+3{y}^{2} + 4y - 4 &\hfill = & \hfill 0 & \text{ }\\3{x}^{2}-6x+3{y}^{2} + 4y &\hfill=& \hfill 4 & \text{ add 4 to both sides }\\3\left({x}^{2} - 2x + 1\right) + 3\left({y}^{2} +\frac{4}{3}y\right) &\hfill = & \hfill 4 & \text{ factor out leading coefficients }\\3\left({x}^{2} - 2x + 1\right) + 3\left({y}^{2} +\frac{4}{3}y + \frac{4}{9}\right) &\hfill = & \hfill 4 +3(1) +3\left(\frac{4}{9}\right) & \text{ complete the square in x, y }\\3{\left(x -1\right)}^{2} + 3{\left(y +\frac{2}{3}\right)}^{2} &\hfill = & \hfill \frac{25}{3} & \text{ factor }\\{\left(x -1\right)}^{2} + {\left(y +\frac{2}{3}\right)}^{2} &\hfill = & \hfill \frac{25}{9} & \text{ divide both sides by 3 }\end{array}\\[/latex-display] From the standard equation of a circle, we can identify x-1 as x-h, so h = 1,and [latex]y + \frac{2}{3}\\[/latex] as y-k, so [latex]k = -\frac{2}{3}\\[/latex]. Hence, the center is (h,k) = [latex]\left(1,-\frac{2}{3}\right)\\[/latex]. Furthermore we see that [latex]{r}^{2} = \frac{25}{9}\\[/latex] so the radius is [latex]\frac{5}{3}\\[/latex].Example 4: Given the endpoints of it's diameter, find the equation of a circle using the Midpoint Formula.
Write the standard equation of a circle given that it's diameter has the endpoints (-1,3) and (2,4).Solution
We recall that a diameter of a circle is a line segment containing the center and two points on the circle. Plotting the given data yields Since the circle passes through the endpoints of the diameter, we know that the midpoint (h , k) of the diameter is the center of the circle. From the midpoint formula, we get[latex]\begin{array}{ccc}M= (h, k) &\hfill= &\hfill\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)\\\text{ }&\hfill=&\hfill\left(\frac{-1+2}{2},\frac{3+4}{2}\right)\\\text{ }&\hfill=&\hfill\left(\frac{1}{2},\frac{7}{2}\right)\end{array}\\[/latex]
The diameter of the circle is the distance between the given points, so we know that half of the distance is the radius. Thus,
[latex]\begin{array}{lll}{ r }&\hfill=&\hfill\frac{1}{2}\sqrt{{\left({x}_{2} - {x}_{1}\right)}^{2}+{\left({y}_{2} - {y}_{1}\right)}^{2}}\\\text{ }&\hfill=&\hfill\frac{1}{2}\sqrt{{\left(2 - (-1)\right)}^{2}+{\left(4 - 3\right)}^{2}}\\\text{ }&\hfill=&\hfill\frac{1}{2}\sqrt{{3}^{2}+{1}^{2}}\\\text{ }&\hfill=&\hfill\frac{\sqrt{10}}{2}\end{array}\\[/latex]
Finally, since [latex]{\left(\frac{\sqrt{10}}{2}\right)}^{2} = \frac{10}{4}\\[/latex], our answer becomes [latex]{\left(x-\frac{1}{2}\right)}^{2}+{\left(y-\frac{7}{2}\right)}^{2}=\frac{10}{4}\\[/latex]Example 5: Identify points on the Unit Circle.
Find the points on the Unit Circle whose y-coordinate is [latex]\frac{\sqrt{3}}{2}\\[/latex].Solution
Replace y with [latex]\frac{\sqrt{3}}{2}\\[/latex]in the equation [latex]{x}^{2} + {y}^{2} = 1\\[/latex] to get[latex]\begin{array}{ccc}\hfill{x}^{2}+{y}^{2}&\hfill=&\hfill{ 1 }\\\hfill{x}^{2} + {\left(\frac{\sqrt{3}}{2}\right)}^{2} &\hfill= &\hfill{ 1 }\\\hfill{x}^{2}+\frac{3}{4}&\hfill=&\hfill{ 1 }\\\hfill{x}^{2} &\hfill= &\hfill{\frac{1}{4}}\\\hfill{x} &\hfill = &\pm\sqrt{\frac{1}{4}}\\\hfill{x} &=&\pm{\frac{1}{2}}\end{array}\\[/latex]
The resulting points on the Unit Circle whose y-coordinate is [latex]\frac{\sqrt{3}}{2}\\[/latex] are [latex]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\text{ and }\left(\frac{-1}{2},\frac{\sqrt{3}}{2}\right)\\[/latex]
Licenses & Attributions
CC licensed content, Shared previously
- Circles - College Algebra 3rd Ed. (2013). Authored by: Carl Stitz, Jeff Zeager. Located at: https://www.stitz-zeager.com/. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike.



