We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

TEXT
Unlock Solution Steps
Sign in to
Symbolab
Get full access to all Solution Steps for any math problem
By continuing, you agree to our Terms of Use
and have read our Privacy Policy

Study Guides > Mathematics for the Liberal Arts

A Bit of Geometry

Learning Outcomes

  • Given the part and the whole, write a percent
  • Calculate both relative and absolute change of a quantity
  • Calculate tax on a purchase
Geometric shapes, as well as area and volumes, can often be important in problem solving. terraced hillside of rice paddies Let's start things off with an example, rather than trying to explain geometric concepts to you.

Example

You are curious how tall a tree is, but don’t have any way to climb it. Describe a method for determining the height.

Answer: There are several approaches we could take. We’ll use one based on triangles, which requires that it’s a sunny day. Suppose the tree is casting a shadow, say 15 ft long. I can then have a friend help me measure my own shadow. Suppose I am 6 ft tall, and cast a 1.5 ft shadow. Since the triangle formed by the tree and its shadow has the same angles as the triangle formed by me and my shadow, these triangles are called similar triangles and their sides will scale proportionally. In other words, the ratio of height to width will be the same in both triangles. Using this, we can find the height of the tree, which we’ll denote by h: [latex-display]\frac{6\text{ ft. tall}}{1.5\text{ ft. shadow}}=\frac{h\text{ ft. tall}}{15\text{ ft. shadow}}[/latex-display]

Multiplying both sides by 15, we get h = 60. The tree is about 60 ft tall.

Similar Triangles

We introduced the idea of similar triangles in the previous example. One property of geometric shapes that we have learned is a helpful problem-solving tool is that of similarity.  If two triangles are the same, meaning the angles between the sides are all the same, we can find an unknown length or height as in the last example. This idea of similarity holds for other geometric shapes as well.

Guided Example

Mary was out in the yard one day and had her two daughters with her. She was doing some renovations and wanted to know how tall the house was. She noticed a shadow 3 feet long when her daughter was standing 12 feet from the house and used it to set up figure 1.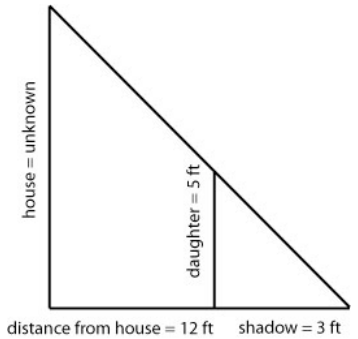
Fig2_3_1 Figure 1.
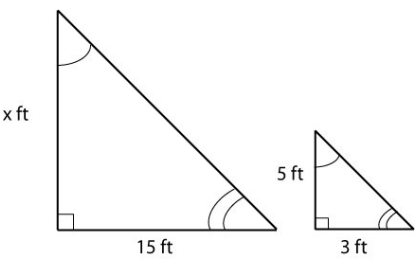We can take that drawing and separate the two triangles as follows allowing us to focus on the numbers and the shapes. These triangles are what are called similar triangles. They have the same angles and sides in proportion to each other. We can use that information to determine the height of the house as seen in figure 2.
Figure 2. Figure 2.
To determine the height of the house, we set up the following proportion: [latex-display]\displaystyle\frac{x}{15}=\frac{5}{3}\\[/latex-display] Then, we solve for the unknown x by using cross products as we have done before: [latex-display]\displaystyle{x}=\frac{5\times{15}}{3}=\frac{75}{3}=25\\[/latex-display] Therefore, we can conclude that the house is 25 feet high.
  It may be helpful to recall some formulas for areas and volumes of a few basic shapes:

Areas

Rectangle Circle, radius r
Area: [latex]L\times{W}[/latex] Area: [latex]\pi{r^2}[/latex]
Perimeter: [latex]2l+2W[/latex]  Circumference[latex]2\pi{r}[/latex]
 
Rectangular Box Cylinder
Volume: [latex]L\times{W}\times{H}[/latex]      Volume: [latex]\pi{r^2}h[/latex]
                                                 
  In our next two examples, we will combine the ideas we have explored about ratios with the geometry of some basic shapes to answer questions.  In the first example, we will predict how much dough will be needed for a pizza that is 16 inches in diameter given that we know how much dough it takes for a pizza with a diameter of 12 inches. The second example uses the volume of a cylinder to determine the number of calories in a marshmallow.

Examples

If a 12 inch diameter pizza requires 10 ounces of dough, how much dough is needed for a 16 inch pizza?

Answer: To answer this question, we need to consider how the weight of the dough will scale. The weight will be based on the volume of the dough. However, since both pizzas will be about the same thickness, the weight will scale with the area of the top of the pizza. We can find the area of each pizza using the formula for area of a circle, [latex]A=\pi{r}^2[/latex]: A 12" pizza has radius 6 inches, so the area will be [latex]\pi6^2[/latex] = about 113 square inches. A 16" pizza has radius 8 inches, so the area will be [latex]\pi8^2[/latex] = about 201 square inches. Notice that if both pizzas were 1 inch thick, the volumes would be 113 in3 and 201 in3 respectively, which are at the same ratio as the areas. As mentioned earlier, since the thickness is the same for both pizzas, we can safely ignore it. We can now set up a proportion to find the weight of the dough for a 16" pizza: [latex-display]\displaystyle\frac{10\text{ ounces}}{113\text{in}^2}=\frac{x\text{ ounces}}{201\text{in}^2}[/latex-display] Multiply both sides by 201 [latex]\displaystyle{x}=201\cdot\frac{10}{113}[/latex] = about 17.8 ounces of dough for a 16" pizza. It is interesting to note that while the diameter is [latex]\displaystyle\frac{16}{12}[/latex] = 1.33 times larger, the dough required, which scales with area, is 1.332 = 1.78 times larger.

The following video illustrates how to solve this problem. https://youtu.be/e75bk1qCsUE

Example

A company makes regular and jumbo marshmallows. The regular marshmallow has 25 calories. How many calories will the jumbo marshmallow have?

Answer: We would expect the calories to scale with volume. Since the marshmallows have cylindrical shapes, we can use that formula to find the volume. From the grid in the image, we can estimate the radius and height of each marshmallow. The regular marshmallow appears to have a diameter of about 3.5 units, giving a radius of 1.75 units, and a height of about 3.5 units. The volume is about π(1.75)2(3.5) = 33.7 units3. The jumbo marshmallow appears to have a diameter of about 5.5 units, giving a radius of 2.75 units, and a height of about 5 units. The volume is about π(2.75)2(5) = 118.8 units3. We could now set up a proportion, or use rates. The regular marshmallow has 25 calories for 33.7 cubic units of volume. The jumbo marshmallow will have: [latex-display]\displaystyle{118.8}\text{ units}^3\cdot\frac{25\text{ calories}}{33.7\text{ units}^3}=88.1\text{ calories}[/latex-display] It is interesting to note that while the diameter and height are about 1.5 times larger for the jumbo marshmallow, the volume and calories are about 1.53 = 3.375 times larger.

For more about the marshmallow example, watch this video. https://youtu.be/QJgGpxzRt6Y

Try It

A website says that you’ll need 48 fifty-pound bags of sand to fill a sandbox that measure 8ft by 8ft by 1ft. How many bags would you need for a sandbox 6ft by 4ft by 1ft?

Answer:

The original sandbox has volume [latex]64\text{ft}^3[/latex]. The smaller sandbox has volume [latex]24\text{ft}^3[/latex]. [latex]\displaystyle\frac{48\text{bags}}{64\text{ft}^2}=\frac{x\text{ bags}}{24\text{in}^3}[/latex] results in x = 18 bags.

Mary (from the application that started this topic), decides to use what she knows about the height of the roof to measure the height of her second daughter. If her second daughter casts a shadow that is 1.5 feet long when she is 13.5 feet from the house, what is the height of the second daughter? Draw an accurate diagram and use similar triangles to solve.

Answer: 2.5 ft

In the next section, we will explore the process of combining different types of information to answer questions.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously